Coefficiente dilatazione lineare acciaio: quanto vale e come calcolarlo
Il coefficiente di dilatazione termica lineare dell’acciaio al carbonio (λ) è uguale a 1,2 x 10^-5 C^-1.
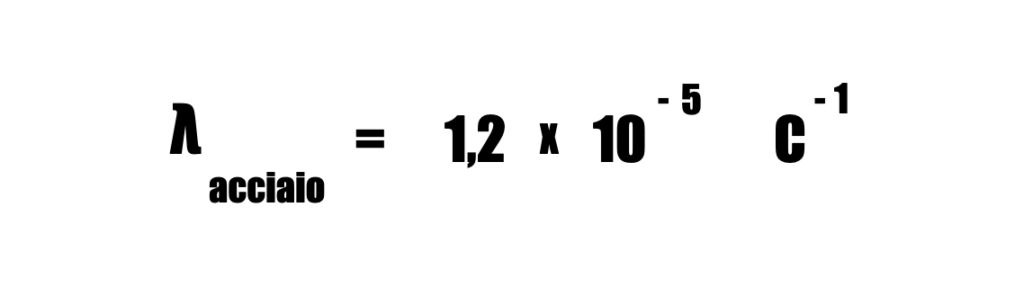
Ma cos’è la dilatazione termica di un materiale?
Come si calcola il coefficiente di dilatazione lineare? E soprattutto perché è fondamentale conoscerlo?
Scorri questo articolo per scoprire:
- Cos’è la dilatazione termica lineare: definizione e formule
- Il coefficiente di dilatazione termica lineare λ
- Tabella dei coefficienti di dilatazione lineare
- Un esempio di calcolo della dilatazione lineare
- Forse non sapevi che…la dilatazione lineare nella vita di tutti i giorni
Cos’è la dilatazione lineare
In fisica, quando un materiale viene riscaldato, gli atomi che lo compongono vibrano con maggiore intensità, causando un’espansione del materiale stesso. Al contrario, quando viene raffreddato, gli atomi vibrano meno intensamente, determinando una contrazione.
La dilatazione lineare (ΔL) è una particolare tipologia di dilatazione termica (a differenza della dilatazione termica o volumica, comprende una sola dimensione lineare) che si riferisce all’aumento o diminuzione della lunghezza di un materiale solido in risposta alle variazioni di temperatura.
Questo fenomeno è una manifestazione delle proprietà termiche del materiale, in particolare del suo coefficiente di dilatazione lineare.
La dilatazione lineare è fondamentale in fisica e ingegneria perché permette di prevedere e gestire i cambiamenti dimensionali dei materiali in risposta alle variazioni di temperatura. Ignorare questo fenomeno potrebbe portare a gravi conseguenze strutturali, come fratture, crepe o malfunzionamenti.
Formula fisica della dilatazione lineare
La dilatazione lineare può essere espressa matematicamente tramite la seguente formula: Δl=λ⋅l0⋅ΔT
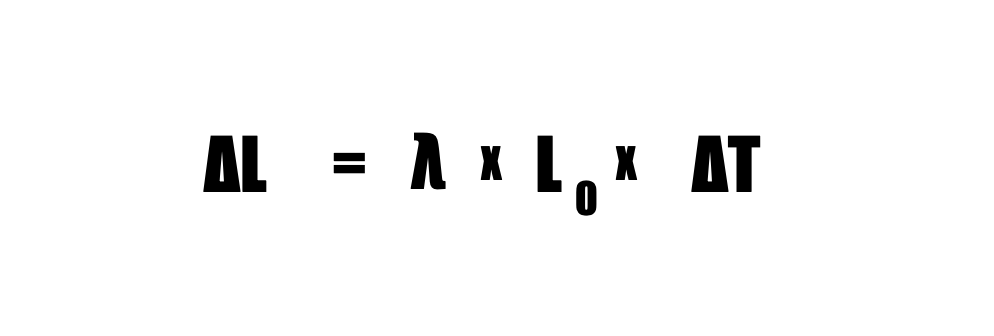
Dove:
- Δl è la variazione di lunghezza del corpo. Rappresenta quanto il materiale si allunga o si contrae a seguito di un cambiamento di temperatura.
- λ è il coefficiente di dilatazione lineare. Questo coefficiente caratterizza quanto un materiale si dilata per ogni grado di variazione della temperatura. È specifico per ogni materiale.
- L0 è la lunghezza del corpo alla temperatura T0. È la lunghezza del materiale prima di qualsiasi variazione di temperatura.
- ΔT è la variazione di temperatura. Indica la differenza di temperatura alla quale il materiale è sottoposto, calcolata come la temperatura finale meno la temperatura iniziale.
In parole semplici, la dilatazione lineare è il fenomeno per cui un materiale si allunga o si accorcia quando cambia la temperatura. Ad esempio, un ponte in acciaio si espande leggermente durante l’estate e si contrae durante l’inverno. Questa espansione e contrazione possono sembrare piccole, ma su grandi strutture possono causare significativi problemi se non vengono considerate in fase di progettazione.
Il coefficiente di dilatazione lineare λ dell’acciaio
Il coefficiente di dilatazione lineare dell’acciaio è un parametro fondamentale per prevedere come questo materiale si espanderà o contrarrà con le variazioni di temperatura. Per l’acciaio, il valore tipico del coefficiente di dilatazione lineare è circa 12×10−6°C−1.
Questo significa che per ogni grado Celsius di incremento di temperatura, ogni metro di acciaio si dilaterà di 12 micrometri.
Cos’è il Coefficiente di Dilatazione Termica
Il coefficiente di dilatazione termica è una misura della capacità di un materiale di espandersi o contrarsi in risposta a variazioni di temperatura. Specificamente, il coefficiente di dilatazione lineare si riferisce alla variazione unidimensionale di lunghezza per unità di lunghezza iniziale per grado di variazione di temperatura. Questo coefficiente è essenziale per comprendere il comportamento termico dei materiali e garantire la loro integrità strutturale e funzionale in applicazioni pratiche.
Coefficiente di dilatazione termica: la formula
Il coefficiente di dilatazione lineare (λ) può essere ricavato dalla formula della dilatazione lineare.
Partendo dalla formula Δl=λ⋅l0⋅ΔT
Per derivare il coefficiente di dilatazione lineare partendo dalla formula della dilatazione lineare, seguiamo questi passaggi:
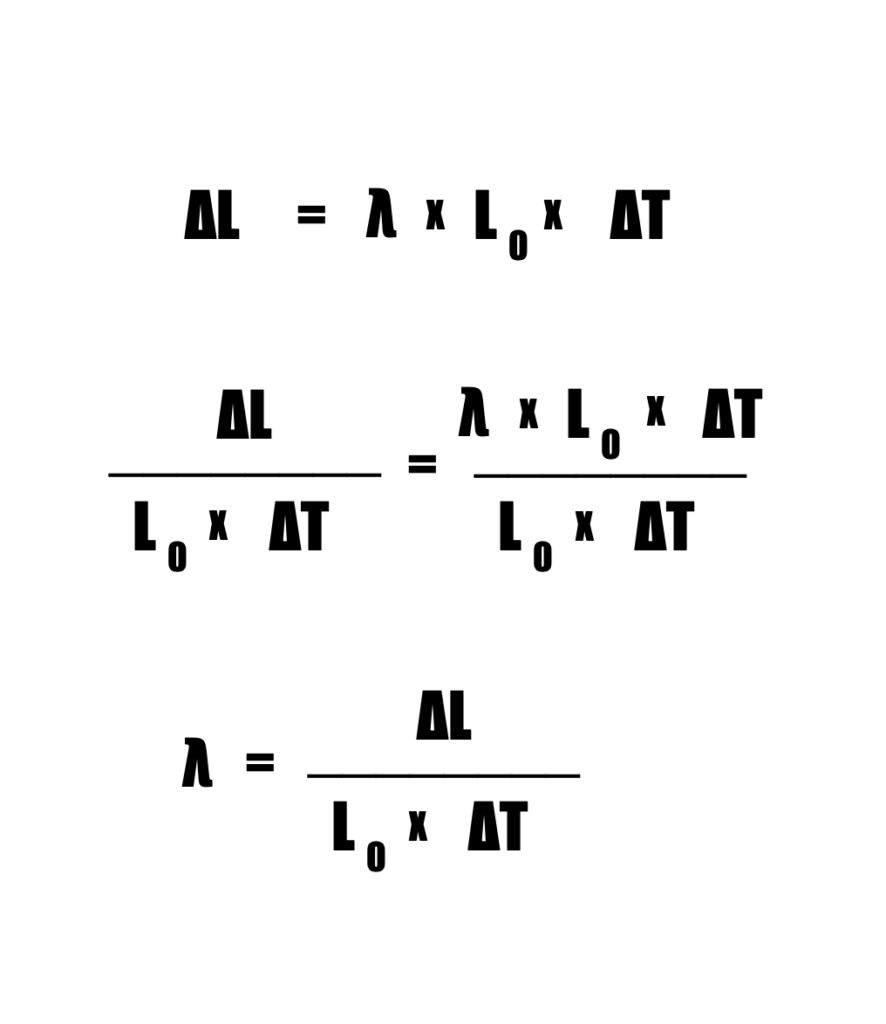
Questa formula ci mostra che λ è il rapporto tra la variazione di lunghezza per unità di lunghezza iniziale e la variazione di temperatura.
Dilatazione termica volumetrica
La dilatazione lineare si riferisce alla variazione della lunghezza di un materiale in risposta a una variazione di temperatura.
Nei casi in cui la dilatazione non interessa solo un lato del materiale (es. una barra d’acciaio), si parla di dilatazione termica volumetrica.
La dilatazione volumetrica si riferisce alla variazione del volume di un materiale in risposta a variazioni di temperatura.
La variazione di volume (ΔV) di un materiale in seguito a una variazione di temperatura (ΔT) può essere espressa con la seguente formula: ΔV=β⋅V0⋅ΔT
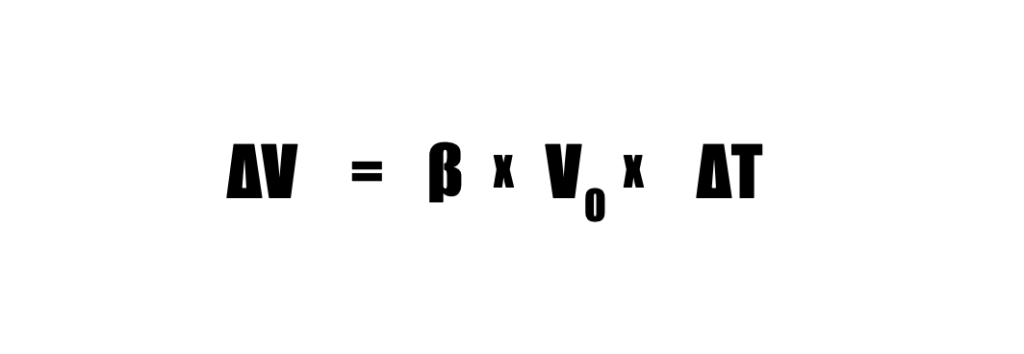
Dove:
- ΔV è la variazione di volume.
- β è il coefficiente di dilatazione volumetrica.
- V0 è il volume iniziale del materiale.
- ΔT è la variazione di temperatura.
La dilatazione volumetrica (ΔV) può essere calcolata a partire dalla dilatazione lineare utilizzando il coefficiente di dilatazione volumetrica (β). Per i materiali isotropi, il coefficiente di dilatazione volumica è approssimativamente tre volte il coefficiente di dilatazione lineare: β≈3α
Tabella dei coefficienti di dilatazione termica lineare
| Materiale | Coefficiente di Dilatazione Lineare (°C⁻¹) |
|---|---|
| Acciaio al carbonio | 1,2 x 10⁻⁵ |
| Acciaio inox | 1,7 x 10⁻⁵ |
| Alluminio | 2,4 x 10⁻⁵ |
| Alluminio leghe | 2,3 x 10⁻⁵ |
| Antimonio | 1,1 x 10⁻⁵ |
| Argento | 1,9 x 10⁻⁵ |
| Bismuto | 1,3 x 10⁻⁵ |
| Bronzo (7,9%) | 1,8 x 10⁻⁵ |
| Bronzo (14%) | 1,8 x 10⁻⁵ |
| Bronzo fosforoso | 1,8 x 10⁻⁵ |
| Cadmio | 3,1 x 10⁻⁵ |
| Cobalto | 1,8 x 10⁻⁵ |
| Conglomerato cementizio | 1,2 x 10⁻⁵ |
| Cromo | 0,8 x 10⁻⁵ |
| Ferro | 1,2 x 10⁻⁵ |
| Ghisa comune | 1,1 x 10⁻⁵ |
| Granito | 0,9 x 10⁻⁵ |
| Legname fibra dolce | 0,4 x 10⁻⁵ |
| Legname forte | 5,8 x 10⁻⁵ |
| Magnesio | 2,2 x 10⁻⁵ |
| Marmi | 0,7 x 10⁻⁵ |
| Mattoni | 0,6 x 10⁻⁵ |
| Mercurio | 18,1 x 10⁻⁵ |
| Molibdeno | 0,5 x 10⁻⁵ |
| Nichel | 1,3 x 10⁻⁵ |
| Oro | 1,5 x 10⁻⁵ |
| Ottone | 1,9 x 10⁻⁵ |
| Piombo | 2,9 x 10⁻⁵ |
| Platino | 0,9 x 10⁻⁵ |
| Polietilene AD | 20 x 10⁻⁵ |
| Polietilene BD | 20 x 10⁻⁵ |
| Polipropilene | 12 x 10⁻⁵ |
| PVC | 7 x 10⁻⁵ |
| Rame | 1,7 x 10⁻⁵ |
| Silicio | 0,8 x 10⁻⁵ |
| Stagno | 2,7 x 10⁻⁵ |
| Tungsteno | 0,5 x 10⁻⁵ |
| Vetro | 0,8 x 10⁻⁵ |
| Vetro Pyrex | 0,3 x 10⁻⁵ |
| Vetro temperato | 0,9 x 10⁻⁵ |
| Zinco | 3,1 x 10⁻⁵ |
Forse non sapevi che…
Forse non sapevi che la dilatazione termica lineare è un fenomeno fisico tanto fondamentale da influenzare molteplici settori e applicazioni quotidiane.
Tra questi: architettura e ingegneria civile (progettazione di edifici, ponti e strade), produzione di materiali compositi (il cemento armato sfrutta il fatto che acciaio e calcestruzzo hanno coefficienti di dilatazione simili, permettendo una coesione stabile tra i due materiali), settore aerospaziale (i componenti degli aerei e dei satelliti devono essere progettati per resistere a variazioni estreme di temperatura senza deformarsi o danneggiarsi), industria meccanica (macchinari e strumenti di precisione devono mantenere tolleranze strette nonostante le variazioni termiche).
Le rotaie dei treni sono soggette a significative variazioni di temperatura, specialmente in regioni con climi estremi. Durante l’estate, le rotaie si espandono a causa del calore, mentre in inverno si contraggono. Per evitare che le rotaie si deformino o si spezzino, si utilizzano giunti di dilatazione, che permettono alle rotaie di espandersi e contrarsi liberamente senza causare danni strutturali. Questi giunti sono essenziali per mantenere la sicurezza e l’efficienza del trasporto ferroviario.


I ponti e i cavalcavia devono anch’essi tener conto della dilatazione termica. Le variazioni di temperatura possono causare espansioni e contrazioni nei materiali da costruzione, portando a potenziali deformazioni strutturali.
Per mitigare questi effetti, i ponti sono progettati con giunti di dilatazione, che permettono alle diverse parti della struttura di muoversi indipendentemente senza compromettere la stabilità complessiva. Questi giunti sono visibili come spazi o coperture flessibili tra le sezioni del ponte, e sono cruciali per garantire la durabilità e la sicurezza della struttura.
Calcolo della dilatazione lineare: esercizio di prova
Come calcolare la dilatazione lineare?
Ecco un esempio di calcolo per mettere alla prova quanto abbiamo visto in questo articolo.
Immagina di avere una trave di acciaio lunga 10 metri. La temperatura iniziale della trave è di 20°C. La temperatura aumenta fino a 50°C.
Calcola la variazione di lunghezza della trave dovuta all’aumento di temperatura.
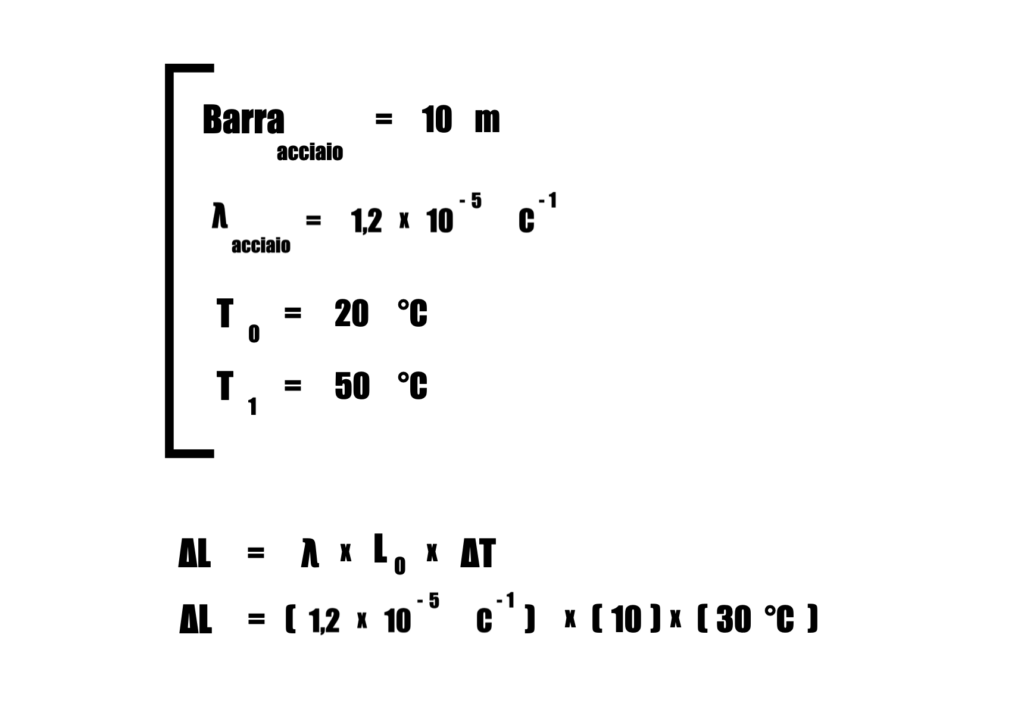
La trave di acciaio si allungherà di 3.6 mm quando la temperatura aumenta da 20°C a 50°C.
Se la temperatura iniziale fosse 10°C e aumentasse fino a 60°C, quale sarebbe la nuova variazione di lunghezza della stessa trave di acciaio?
Come cambierebbe la variazione di lunghezza se la trave fosse lunga 20 metri invece di 10 metri con le stesse variazioni di temperatura?




