Tensione ammissibile e tensione di snervamento: caratteristiche meccaniche dell’acciaio
Tensione ammissibile e tensione di snervamento dell’acciaio: due caratteristiche meccaniche di assoluta importanza nel campo dell’ingegneria per il progetto di costruzioni.
Competenza e sicurezza passano dalla conoscenza profonda dell’argomento.
In questo articolo, Prontuario Online mette a tua disposizione formule e spiegazioni, calcoli e tabelle, una guida completa sulla tensione ammissibile e sullo snervamento acciaio a partire dai loro valori, di seguito consultabili:
| Classe acciaio | Tensione di snervamento | Tensione a rottura |
|---|---|---|
| S235 (Fe 360) | 235 N/mm2 | 360 N/mm2 |
| S275 (Fe 430) | 275 N/mm2 | 430 N/mm2 |
| S355 (Fe 510) | 355 N/mm2 | 510 N/mm2 |
| S450 | 440 N/mm2 | 550 N/mm2 |
Tensione ammissibile: di cosa si tratta?
In ingegneria civile e meccanica per il progetto di costruzioni, con tensione meccanica ci si riferisce al valore della massima tensione a cui un materiale duttile può essere sottoposto con sicurezza nelle condizioni operative.
Relativamente alla tensione ammissibile, la necessità di conoscere le caratteristiche meccaniche del materiale, al fine di una idonea progettazione strutturale, ci porta alla prova di trazione, una prova distruttiva da cui si ricava una tabella che evidenzia i valori di allungamento relativamente ad una forza applicata, fino alla rottura del pezzo.
Interessando i dati relativi al materiale in sé le forze vengono divise per l’area di sezione del campione e gli allungamenti per lunghezza iniziale, ottenendo in questo modo una corrispondenza fra tensioni meccaniche:
(σ = F/A)
e allungamenti relativi
(ε = Δl/l0)
σ – tensioni corrispondenti
ε – allungamenti relativi
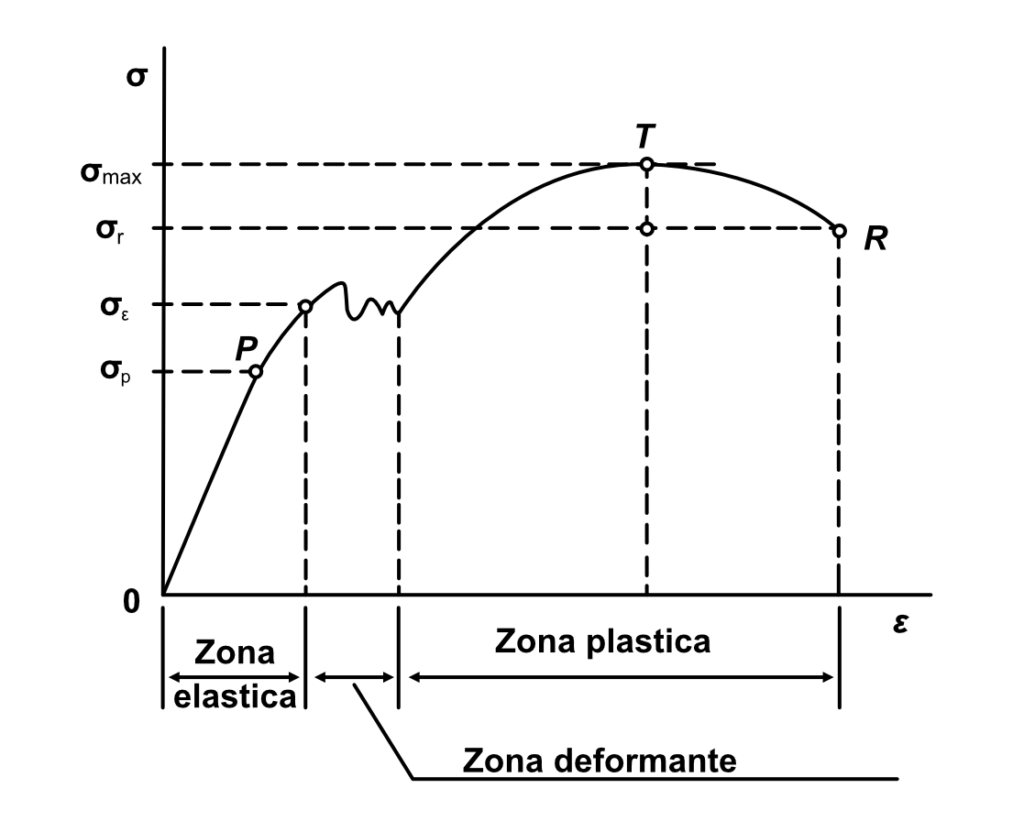
La corrispondenza risulta più evidente costruendo un grafico che riporti in ascissa gli allungamenti relativi ε e in ordinata le tensioni σ.
Per materiali duttili, come l’acciaio, il grafico inizia con un tratto quasi rettilineo, in cui σ ed ε sono direttamente proporzionali secondo una costante “E” (σ = E·ε), poi piega bruscamente fino a diventare pressoché orizzontale; prosegue con alcune oscillazioni e ricomincia a salire fino a interrompersi quando si raggiunge la rottura.
Il tratto in cui vale la proporzionalità fra σ ed ε è quello elastico, il punto in cui la curva piega e smette di essere rettilinea, quando cioè smette di valere la legge di proporzionalità, è quello in cui il materiale smette di comportarsi in modo elastico, ma inizia a deformarsi in maniera permanente. Questo punto individua la cosiddetta “tensione di snervamento”.
Tensione di snervamento
La tensione di snervamento è quel valore di tensione che, applicato ad un corpo, produce delle deformazioni irreversibili e di conseguenza ne modifica la forma, quasi sicuramente rendendolo inadatto allo scopo per cui è stato progettato.
Inoltre, una volta che un componente meccanico entra nella fase plastica, diventa molto più difficile prevedere qual è il margine prima di arrivare alla rottura.
Si capisce quindi che la conoscenza della tensione di snervamento costituisce un dato molto importante nella progettazione.
Se però si guarda con attenzione una curva vera, si trova che il tratto iniziale, quello elastico, non è veramente rettilineo, e che anche la piega che mostra il passaggio dal tratto elastico a quello successivo non avviene in un punto preciso: il grafico in realtà è una curva, inizialmente quasi rettilinea, ma che gradualmente diviene sempre più accentuata. Questo fatto è dovuto alla presenza di dislocazioni all’interno del materiale, cioè imperfezioni nel reticolo cristallino dei “grani” o “cristalli” che compongono un materiale metallico; quando si applica una forza ad un componente, le dislocazioni iniziano a muoversi, provocando delle piccole deformazioni irreversibili.
Non per questo si deve considerare che il pezzo sia entrato nello snervamento, ma dovrebbe essere chiaro che la deformazione plastica si presenta con gradualità, inizialmente in misura modestissima, poi via via sempre più importante quanto più alta è la forza applicata: infatti esistono dislocazioni di tipo diverso, nonché relative a piani cristallini con diversi orientamenti rispetto alla direzione della forza applicata, per cui alcune si muovono per forze piccole, altre richiedono una maggiore spinta per cominciare a far scorrere gli atomi; ad un certo punto la gran parte delle dislocazioni si può muovere e il risultato è una deformazione macroscopica, rilevabile su un campione della prova di trazione con i normali strumenti di misura (micrometri o calibri), e allora si parla di snervamento.
Come stabilire la tensione di snervamento
Per stabilire quale sia il valore della tensione di snervamento normalmente si considera quello per cui la curva si è discostata di una certa percentuale dalla retta ideale:
σ = E·ε
Di solito si usa lo 0,2%, tanto che in molte tabelle non si trova il simbolo σs, bensì fp 0,2.
Questo per chiarire che la tensione di snervamento è una convenzione che non discende da un dato assoluto ed oggettivo. Eseguendo più prove su campioni diversi è del tutto normale riscontrare valori diversi di fp 0,2 nonché della tensione di rottura.
Prendendo come esempio una tabella relativa ad un acciaio da costruzione “S235JR” si riscontra che, per spessori minori di 3 mm la tensione di rottura è compresa tra 360 e 510 MPa, mentre per spessori da 3 a 100 mm varia da 340 a 470 MPa. Si tratta di variazioni importanti, assumere in generale che la tensione di rottura sia pari a 360 MPa è un arbitrio, e che se il materiale disponibile in realtà regge fino a 510 MPa, la progettazione porterà a un inutile e costoso sovradimensionamento.
Non per questo dobbiamo stabilire che la progettazione meccanica sia sbagliata o inutile, possiamo però acquisire che i limiti di conoscenza della particolare partita di materiale rimangono poco definiti e la possibilità di definirli maggiormente moltiplicando il numero di prove rimane fuori discussione perché, come già precisato, sono distruttive, oltre che lunghe e costose.
A fronte di questo è necessario assumere dei valori cautelativi …oltre che veritieri, tali da ottenere componenti affidabili.
Fondamentale tenere in considerazione la criticità di una soluzione, avere chiara le conseguenze nell’eventualità in cui un dato componente smettesse di funzionare per deformazione o rottura.
Generalmente i produttori forniscono valori di tensione, snervamento e di tensione di rottura che costituiscono un ragionevole estremo inferiore delle prove svolte, il progettista, da parte sua, deve tenere conto dell’esistenza di un’incertezza sulle caratteristiche materiche, e tenerla in considerazione.
In fase di progettazione vi sono ulteriori incertezze legate all’imperfetta capacità di calcolare gli effettivi valori di tensione, ricordiamo che σ e τ sono funzioni della posizione e le equazioni che ne determinano i valori sono note, ma in generale non risolvibili da un punto di vista matematico.
Per questo la progettazione non si può svolgere nel modo più ovvio, cioè individuare delle forme geometriche tali che la tensione massima che si riscontra in un corpo sia inferiore a quella di snervamento del materiale:
σ mass<σs
ma si usa introdurre un coefficiente che riduca i valori di snervamento dichiarati in modo da poter ritenere che non si arrivi a perdite di funzionalità o, peggio, al collasso.
Coefficiente Grado di Sicurezza e Snervamento
Coefficiente detto “grado di sicurezza”, più è elevato e maggiormente ci tutela da errori anche se, ovviamente, induce un sovradimensionamento.
Nel caso di materiali fragili (ceramici, legno …ghisa grigia) non esiste snervamento e si utilizza come riferimento la tensione di rottura. La cautela consiste nell’utilizzare un grado di sicurezza rispetto alla rottura (gR), e il fine che ci poniamo in fase di progettazione è dato dalla disequazione:
σmass ≤ σR / gR
Per materiali duttili (materiali metallici), è giusto riferirsi alla tensione di snervamento, per le ragioni già esposte. Il fine che ci poniamo è di soddisfare la disequazione:
σmass ≤ σs / gs
Come ottenere la tensione ammissibile
Il secondo membro della disequazione è una tensione arbitrariamente ridotta, “tensione ammissibile”, è una tensione limite da non superare per considerare sicuro il risultato della progettazione.
Questa tensione ammissibile non è una caratteristica del materiale e non si può individuare in una curva sforzo-deformazione e nemmeno può essere evidenziata per mezzo di alcuna prova tecnologica.
Valore meccanico della tensione ammissibile
Con tensione ammissibile ci riferiamo ad un valore convenzionale da considerare come limite di sicurezza.
Quindi, definito:
σamm = σR / gR oppure σamm = σs / gs
si può dire che la progettazione deve soddisfare la disequazione:
σmass ≤ σamm
Si può assumere, anche per i materiali duttili, un grado di sicurezza rispetto alla rottura, cioè usare la stessa disequazione dei materiali fragili; in questo caso il valore da adottare per gR dev’essere più grande di quello che si può usare per gs.
Questo criterio nasconde però l’effettiva distanza dallo snervamento quindi è meno razionale.
Utilizzando ancora come esempio l’acciaio S235 per il quale le normative forniscono valori anche della tensione ammissibile:
σs nominale 235
σR nominale 360
σamm spessore≤40 mm 160
σamm spessore>40 mm 140
Alla tensione ammissibile vengono dati valori diversi, considerando che il controllo della produzione dell’acciaio è più difficile per spessori maggiori. Immaginando di usare un componente di spessore inferiore a 40 mm, si deduce che il grado di sicurezza consigliato dalla normativa è:
gs = σs / σamm = 235 / 160 = 1,47 ≃ 1,5
per spessori superiori, invece, il grado di sicurezza consigliato aumenta:
gs = σs / σamm = 235 / 140 = 1,68 ≃ 1,7
Ovviamente è possibile definire il grado di sicurezza rispetto alla rottura, che si troverà come:
gR = σR / σamm = 360 / 160 = 2,25 ≃ 2,3
per spessori fino a 40 mm
gR = σR / σamm = 360 / 160 = 2,57 ≃ 2,6
per spessori oltre i 40 mm.
In pratica, assumere la tensione di snervamento e dividerla per 1,5 oppure quella di rottura e dividerla per 2,3 porta allo stesso risultato.
Un altro aspetto della tensione ammissibile è relativo alle cifre significative: trattandosi di un valore convenzionale, non si può pretendere di definire questo valore con un numero di cifre eccessivo… se si dispone di una tensione di snervamento pari a 235 MPa e si assume il grado di sicurezza pari a 1,5, il risultato è una tensione ammissibile:
σamm = 235 / 1,5 = 156,667 MPa
Di questo numero non ha alcun senso conservare non solo le cifre decimali, ma nemmeno l’unità: se si superano i 157 MPa piuttosto che i 156,7 non succederà verosimilmente niente.
E’ anzi più sensato approssimare il valore a 160 MPa. Si decide insomma che per non avere problemi sarà bene non superare i 160 MPa in alcun punto del componente; il che comporta, data l’imperfetta conoscenza del comportamento del materiale e dell’effettiva distribuzione di tensioni al suo interno, che sarà praticamente impossibile arrivare ad una sensibile condizione di snervamento in qualche punto.
Deve valere l’uguaglianza:
σamm = σs / gs = σR / gR
da cui, prendendo gli ultimi due termini:
σR / σs = gR / gs
ovvero il rapporto fra le tensioni di rottura e di snervamento dev’essere pari a quello fra i rispettivi gradi di sicurezza, al fine di ottenere lo stesso valore della tensione ammissibile con i due metodi. Nel caso dell’acciaio S235, il rapporto fra le tensioni è:
σR / σs = 360 / 235 ≃ 1,53
Si prendono ora le caratteristiche di un acciaio da bonifica come il C40, secondo la normativa, per spessori da 8 a 20 mm:
σs = 400 MPa
σR = 630÷780 MPa
La normativa fornisce un valore per lo snervamento e un intervallo per la rottura; se si vuole calcolare la tensione ammissibile a partire dallo snervamento si può prendere ad esempio un grado di sicurezza come quello già visto in precedenza pari a 1,5:
σamm = σs / gs = 400 / 1,5 = 266,667 MPa ≃ 270 MPa
Se si vuole partire dalla tensione di rottura, però, occorre osservare che il valore inferiore è pari a circa 1,5 volte quello di snervamento, quindi usando un grado di sicurezza gR intorno a 1,5 volte gs, cioè 2,3, si perviene allo stesso risultato:
σamm = σR / gR = 630 / 2,3 = 273,91 MPa ≃ 270 MPa
Se invece si parte dal valore superiore dell’intervallo di tensioni di rottura, evidentemente si arriverà ad un risultato molto diverso:
σamm = σR / gR = 780 / 2,3 = 339,13 MPa ≃ 340 MPa
Se l’acciaio con cui si deve lavorare ha effettivamente un carico di rottura di 780 MPa, usando una tensione ammissibile di 340 MPa si va molto più vicino allo snervamento, per cui il rischio che il componente perda la sua funzionalità è più alto.
Il rapporto fra tensioni di rottura e di snervamento può variare, fra i diversi tipi di acciaio, ma anche per lo stesso, in un intervallo non molto ampio, ma comunque abbastanza importante da rendere poco chiara la scelta di un grado di sicurezza relativo alla rottura. La tabella seguente mostra alcuni esempi:
| S235JR | C40 | 34 CrNiMo 6 | 48 Si 7 | |||||
|---|---|---|---|---|---|---|---|---|
| σs MPa | 235 | 235 | 400 | 400 | 1000 | 1000 | 1110 | 1110 |
| σR MPa | 360 | 510 | 630 | 780 | 1200 | 1400 | 1300 | 1550 |
| σR/σs | 1,53 | 2,17 | 1,58 | 1,95 | 1,20 | 1,40 | 1,17 | 1,40 |
L’ultimo caso riguarda un acciaio per molle, ed è dunque un caso estremo.
Tutto questo comporta la necessità di una scelta adeguata del grado di sicurezza.
La fatica del materiale
Quando il componente è parte di un meccanismo e di conseguenza destinato al movimento, di norma le forze agenti su di esso variano nel tempo; questo si evidenzia maggiormente sui componenti rotanti, come gli alberi: la forza che carica un albero in flessione, rimanendo costante durante la rotazione, rispetto all’albero stesso gira, per cui questo componente si trova inflesso prima in un senso e poi nel senso opposto.
La dinamica genera delle sollecitazioni periodiche che possono provocare il collasso del pezzo. Questo “collasso” parte da microscopiche imperfezioni del materiale, che danno luogo a punti in cui la tensione raggiunge ad ogni ciclo valori molto elevati, fino a ingrandire le lesioni stesse. Dentro il componente, quindi, man mano che la sollecitazione periodica prosegue, si propagano queste lesioni che portano alla rottura senza che si verifichi una deformazione plastica macroscopica.
La fatica è dunque un fenomeno di rottura pericoloso, in quanto può avvenire senza segnali di preavviso. È anche un fenomeno complesso, perché obbliga a mettere in relazione la tensione che si raggiunge dentro il corpo con la durata della vita residua, vale a dire che a seconda del valore delle tensioni che si producono durante il funzionamento la rottura per fatica può avvenire prima o dopo. Quindi lo stesso pezzo può essere adatto a svolgere una data funzione per dieci anni, ma non per venti.
Oltre alla vita residua, diversi parametri influiscono sulla resistenza a fatica, alcuni dipendenti dal materiale, altri dalle dimensioni del componente (più o meno grande) e dalla sua forma (con geometria più o meno articolata, con intagli o senza), altri dalla lavorazione (ad esempio una superficie scabra favorisce l’innesco di microcricche), altri ancora dall’andamento nel tempo delle forze periodiche.
In una fase di dimensionamento preliminare, come del resto (per altri motivi) nello studio scolastico, generalmente non si riesce a considerare questi aspetti, per cui si adopera una tensione ammissibile particolare, ottenuta per mezzo di un grado di sicurezza particolarmente elevato. Innanzitutto diviene obbligatorio partire dalla tensione di rottura e non più da quella di snervamento, dal momento che il fenomeno è dato da una rottura con modalità fragili (assenza di plasticizzazione macroscopica); poi, il coefficiente di sicurezza deve tener conto del fatto che esistono numerosi fattori che concorrono ad abbassare la tensione ammissibile, pur senza entrare nel dettaglio di quantificare ciascuno di essi.
Questi motivi inducono, in un caso semplificato (appunto, dimensionamento preliminare o studio di livello scolastico) a fare un’assunzione empirica, cioè moltiplicare per tre il grado di sicurezza statico, considerando così di raggiungere la sicurezza che il componente abbia una vita residua ragionevole; nei manuali questo grado di sicurezza relativo alla fatica viene indicato con “nR” per distinguerlo dal grado statico gR. In realtà, anche in un caso semplificato è possibile effettuare alcune scelte che possono migliorare l’approssimazione: così un albero rotante viene sollecitato dalla stessa forza in un senso e poi nel senso opposto, mentre un perno fisso su cui ruoti un qualche componente, può ricevere una forza periodica in un senso, ma normalmente non risente di una spinta in senso opposto. Nel primo caso il pezzo è sollecitato da un forza variabile da +F a -F; nel secondo caso la forza varia da +F a zero, ed è quindi meno gravosa. Di conseguenza nel primo caso si può moltiplicare il grado di sicurezza per tre, nel secondo per tre mezzi.
La tensione ammissibile che si ottiene è dunque molto diversa e può condurre a scegliere dimensioni diverse per un componente, con riduzione di pesi, ingombri e costi. È bene ricordare che il progetto esecutivo di un componente o di un assieme può risultare molto complesso e non è detto che sia possibile o conveniente eseguirlo completamente secondo i criteri più raffinati: può risultare conveniente, anche rispetto ai tempi ed ai costi di progettazione, svolgere un dimensionamento preliminare semplificato sulla cui base abbozzare dei disegni; quindi passare alla definizione dei particolari e infine svolgere la verifica nel modo più preciso. Ovviamente si suppone che le fasi precedenti, svolte correttamente, permettano di verificare che non ci sono problemi. Ecco quindi che un criterio semplificato, ma sufficientemente attinente alla realtà, pur su una base empirica, può risultare prezioso.
Per finire i valori consigliabili per acciai laminati o fucinati (la gran maggioranza dei casi) si possono riassumere con una tabella:
| Caso statico | Fatica | ||
|---|---|---|---|
| Alternata | Pulsante (dallo zero) | ||
| gs | gR | nR | nR |
| 1,5/2 | 2,3/3 | 6/9 | 3,5/5,5 |




